Exercise 4: Page Rank Algorithm

Introduction

One of the most vital concepts behind how Google ranks all the indexed websites is the so called «Page Rank Algorithm». First introduced and patented by Larry Page in 1998^¹, this algorithm describes a method to assign a weight to every page in the index, depending on how many other pages link to that page and on the weight of these pages. In this article we’ll cover the mechanics of the algorithm itself and some mathematical basics on which the algorithm is based on.

Eigenvalue and Eigenvectors

In order to better understand the mathematics behind, we need to very briefly introduce a topic called «Eigenvalue/Eigenvector» first. Let’s assume we have the following Matrix:

$A=\begin{bmatrix}1 & 2 \\ 3 & 0\end{bmatrix}$

Now, if we have a vector $\vec{x}$ which is not the null vector, then the following equation with the Eigenvalue represented by $\lambda$ must be valid:

$A\vec{x}=\lambda\vec{x}$

What is this good for? Various things. In geometric terms for example, Eigenvectors will be affected by a transformation matrix in that they are only scaled (by their corresponding Eigenvalue $\lambda$ )but not transformed in any other way, as Trefor Bazett explains it nicely in his video^². In algebraic terms, we can use Eigenvalues to find out if a matrix is diagonizable. Diagonalized matrices are much easier to work with.

The Markov-Chain

Essential to the understanding of the Page Rank Algorithm is the so-called «Markov-Chain». It describes a state-transformation matrix which holds the weights of an adjacency graph. Every weight represents the probability with which the described system will change its current state to another. Let’s have a look at the following graph to get a clearer picture:

State Changes

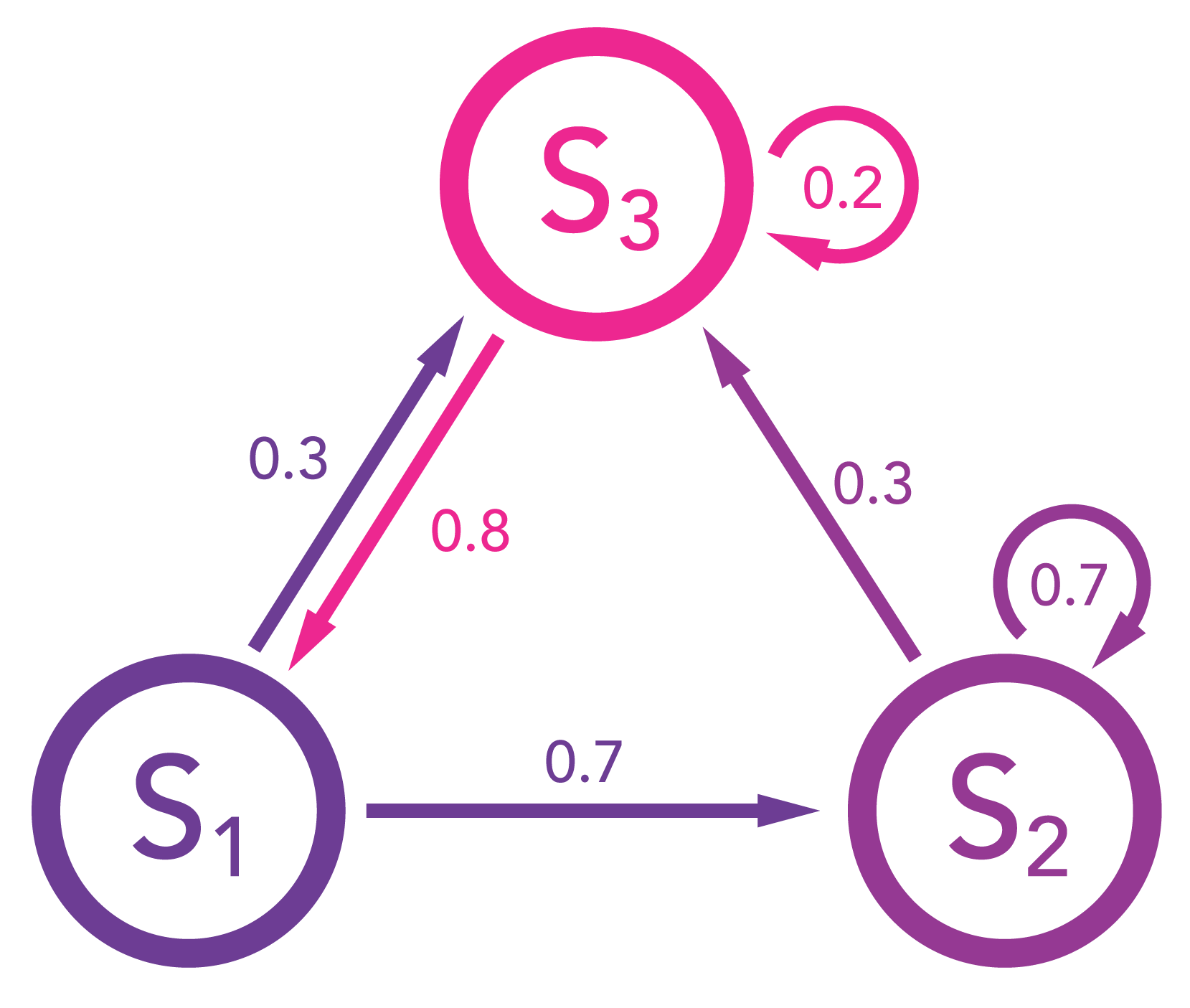
This diagram shows three stages $S_{1}, S_{2}$ and $S_{3}$ . The weights of the graph show the probabilities of every state to change into another. $S_{2}$ and $S_{3}$ can stay unchanged, whereas $S_{1}$ will always change into another state. The outbound weigths of every state sum up to 1.

Now, if we were to represent this model mathematically, we can use a vector $\vec{s}$ to represent the probability of the state in which we see ourselves at this very moment, and use an $n x n$ matrix to represent the probabilities with which the current state will change into another. Let’s assume that in the beginning, our system is in state $S_{1}$ :

$\vec{s}(0) = \begin{bmatrix}1\\0\\0\end{bmatrix}, M= \begin{bmatrix} 0 & 0 & 0.8 \\ 0.7 & 0.7 & 0 \\ 0.3 & 0.3 & 0.2 \\ \end{bmatrix}$

As you can see, the columns of matrix $M$ represent the states $S_{1}$ to $S_{3}$ where we start at, and the rows represent the states $S_{1}$ to $S_{3}$ where we want to go to. So, if we multiply our transformation matrix $M$ with our initial state vector $\vec{s}(0)$ , we’ll get the following outcome:

$\vec{s}(1) = M \cdot \vec{s}(0) = \begin{bmatrix} 0 & 0 & 0.8 \\ 0.7 & 0.7 & 0 \\ 0.3 & 0.3 & 0.2 \\ \end{bmatrix} \cdot \begin{bmatrix}1\\0\\0\end{bmatrix} = \begin{bmatrix}0\\0.7\\0.3\end{bmatrix}$

In other words: after one iteration (in practice, an iteration could represent one hour, one day or any other unit describing the interval of one state change), our system will be in state $S_{2}$ with a 70% chance, or in the state $S_{3}$ with a 30% chance.

How would be account for 3 iterations? Simple:

$\vec{s}(3) = M \cdot \vec{s}(0) = \begin{bmatrix} 0 & 0 & 0.8 \\ 0.7 & 0.7 & 0 \\ 0.3 & 0.3 & 0.2 \\ \end{bmatrix} \cdot ( \begin{bmatrix} 0 & 0 & 0.8 \\ 0.7 & 0.7 & 0 \\ 0.3 & 0.3 & 0.2 \\ \end{bmatrix} \cdot ( \begin{bmatrix} 0 & 0 & 0.8 \\ 0.7 & 0.7 & 0 \\ 0.3 & 0.3 & 0.2 \\ \end{bmatrix} \cdot \begin{bmatrix}1\\0\\0\end{bmatrix} )) = \begin{bmatrix}0.216\\0.511\\0.273\end{bmatrix}$

After 3 iterations, we’ll find ourselves in state $S_{1}$ with a 22% chance, in state $S_{2}$ with a 51% chance and in state $S_{3}$ with a 27% chance. In a more general context we can write:

$\vec{s}(n) = M \cdot (M \cdot (... \cdot (M \cdot \vec{s}(0)))) = M^{n} \cdot \vec{s}(0)$

The interesting question now of course is: What happens if we continue the iterations eternally, i.e. how will the resulting state behave for $n=\infty$ ? The following diagram shows the results for various values for $n$ :

State Changes

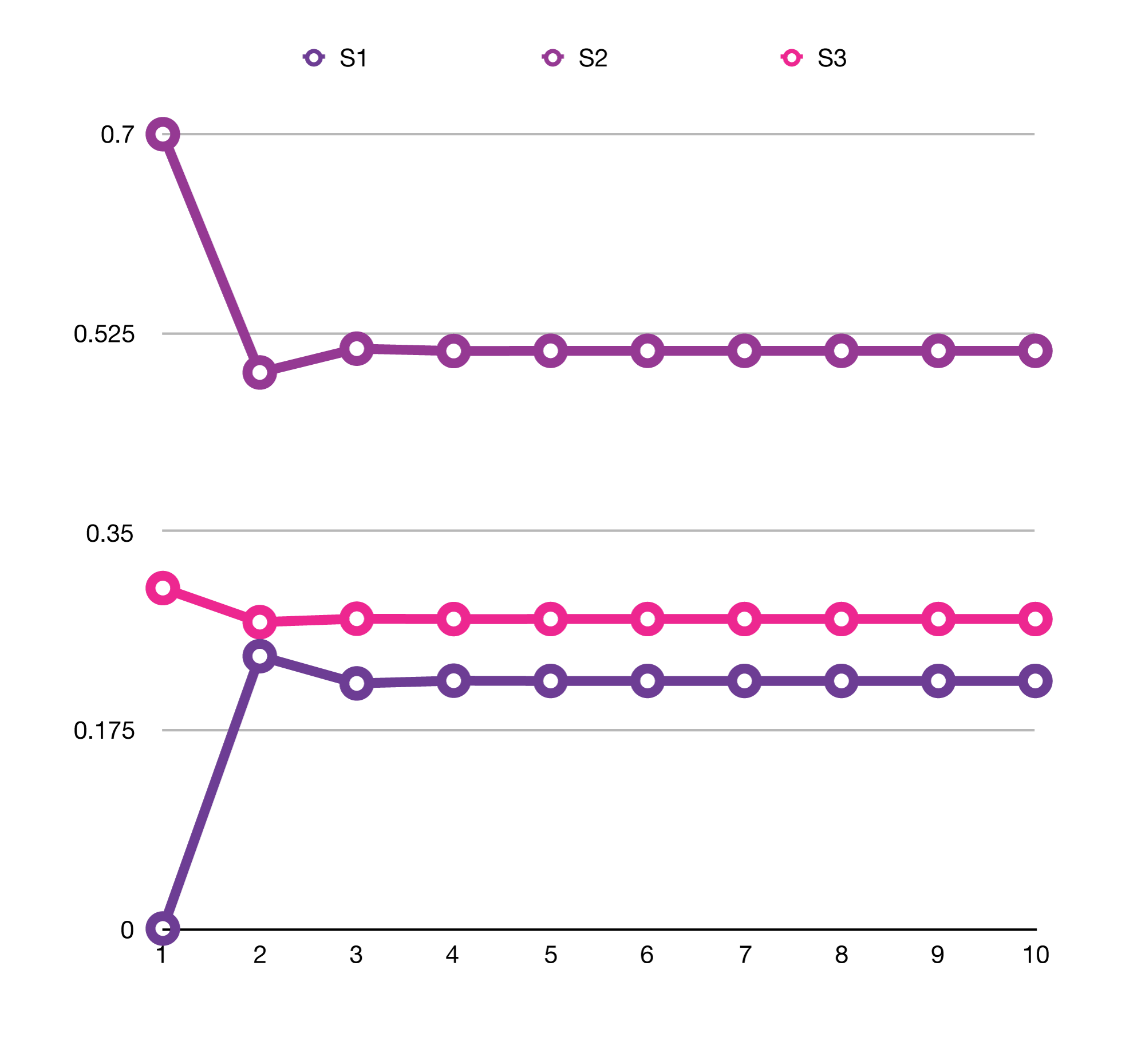
As you can see, the probabilities for the individual states converge to a value in which the system will be «stable» and stay the same, no matter how many more iterations will follow.

Basic principle of the Page Rank Algorithm

Now that we have a basic understanding of the Markov-Matrix, let’s dig into the mechanics of the Page Rank Algorithm. Let’s assume that we have five web pages $W_{1}$ to $W_{5}$ like so:

State Changes

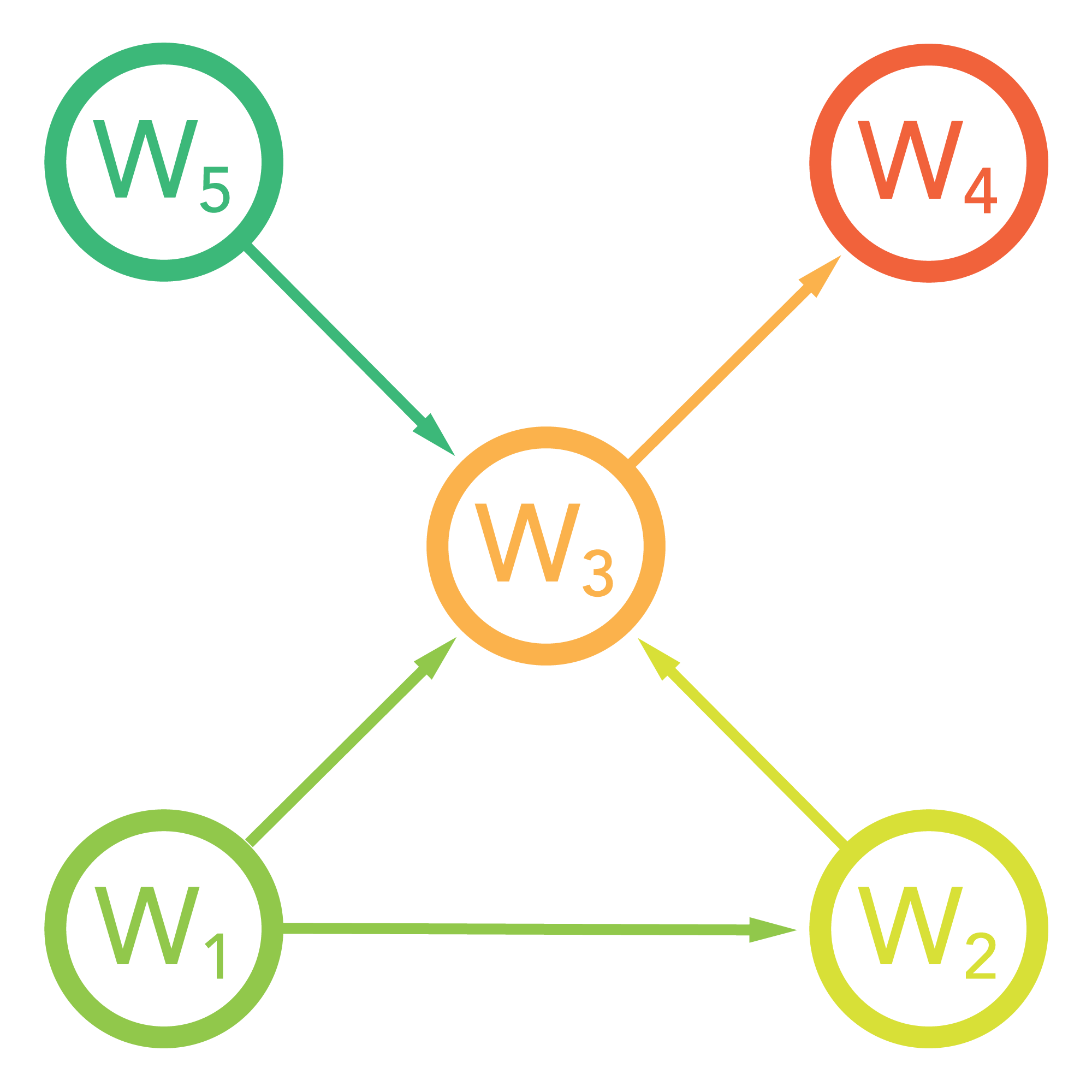
Notice, that this describes a directed graph with the arrows representing hyperlinks to other web pages. From this, we can derive the following adjacency matrix:

$M = \begin{array}{cc} & \begin{array}{ccccc} W_{1} & W_{2} & W_{3} & W_{4} & W_{5} \end{array} \\ \begin{array}{c} W_{1} \\ W_{2} \\ W_{3} \\ W_{4} \\ W_{5} \end{array} & \left(\begin{array}{ccccc} 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 1 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 1 & \quad 1 & \quad 0 & \quad 0 & \quad 1 \\ 0 & \quad 0 & \quad 1 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \end{array}\right) \end{array}$

The basic concept behind the algorithm is to let every web page give their votes for other pages by mentioning them in a hyperlink. So, the more pages link to a specific page the higher this page gets weighed, i.e. «ranked». If we define that every page has an initial weight of 1 and that every inbound link increases that weight by 1, then our diagram would look the following:

State Changes

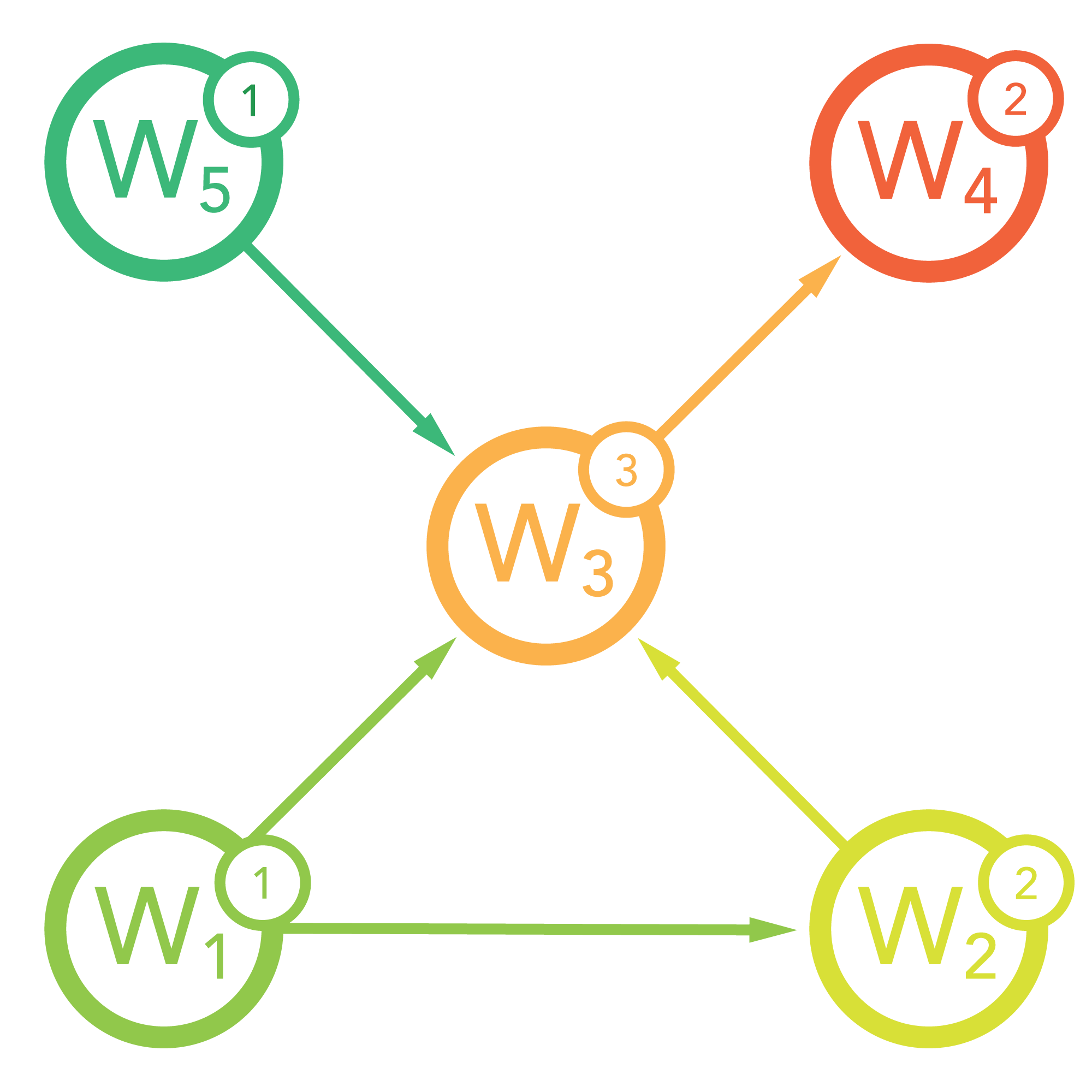
Currently, if we put this situation into an equation to calculate the weight of one specific page, we would get:

$w_{i} = \sum_{j=1}^{n} M_{ji}$

However, this setup would be very easy to manipulate just by adding a ton of links to a page pointing to the web page for which you want to have a good rating. In order to eliminate this flaw, we give every page a total vote of 1 which it distributes evenly over all outbound links:

$w_{i} = \sum_{j=1}^{n} \frac{M_{ji}}{n_{j}}$

whereas $n_{j}$ represents the number of links on page $j$ . So, on pages that have hunders of links (e.g. indexing pages) a link to your page is literally «worth less» than a link from a page with only three links in total.

Still, one could create numerous individual pages with just one link and then point these pages to the page that should get a lot of votes. In order to mitigate this risk, one further measure is added to the equation: the weight of the issuing page itself:

$w_{i} = \sum_{j=1}^{n} \frac{M_{ji}}{n_{j}} w_{j}$

Put into words, this means: The more votes a specific page has, i.e. the more popular a page is, the higher the value of votes it gives to other pages. Now, the formula above creates sort of a circular dependency because we are calculating the weight $w_{i}$ from another weight $w_{j}$ . But how and when is the weight $w_{j}$ calculated? Well, from another weight. But … where does this chain start? It starts at every page having the initial weight of 1. Then, we use a Markov-Chain to develop the weights iteration by iteration. It’s as if we had a block of stone and we use sand paper to grind it down to a sculpture. And the finished sculpture represents the «stable» state of our system.

Now, we know from the previous section that somewhere in eternity, our Markov-Chain will end up in this perfect equilibrium, where nothing has to be added or removed anymore and where the input state corresponds to the output state. This is represented by the Eigenvalue-equation:

$A\vec{w}=\lambda\vec{w}, \lambda = 1$

If we were to calculate the corresponding Eigenvector (to Eigenvalue of 1) then we could just go ahead and resolve the following system of linear equations:

$(A - \mathbb{I})\vec{w} = 0$

But we must not forget that today, there are millions if not billions of web pages out there. Which means that we would have to solve a system of that number of equations (which probably could be efficient with quantum computers…). So instead, we use the approximation by iteration we showed with the Markov-Chain:

$\vec{w}(n) = M^{n} \cdot \vec{w}(0)$

Let’s go back to our initial adjacency matrix and execute that iteration to see what happens. First, we need to adapt the matrix to contain partial votes:

$M = \begin{array}{cc} & \begin{array}{ccccc} W_{1} & W_{2} & W_{3} & W_{4} & W_{5} \end{array} \\ \begin{array}{c} W_{1} \\ W_{2} \\ W_{3} \\ W_{4} \\ W_{5} \end{array} & \left(\begin{array}{ccccc} 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0.5 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0.5 & \quad 1 & \quad 0 & \quad 0 & \quad 1 \\ 0 & \quad 0 & \quad 1 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \end{array}\right) \end{array}$

Our initial state vector $\vec{w}(0)$ is:

$\vec{w}(0) = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}$

After five iterations, our state looks like this:

$\begin{bmatrix} 0 & 0 & 0 & 0 & 0 \\ 0.5 & 0 & 0 & 0 & 0 \\ 0.5 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}^{5} \cdot \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$

Oh snap! Where did all our votes go?? Well, if you look at the diagram again you’ll see that $W_{4}$ marks kind of a dead end. If you follow the links you will eventually end up at $W_{4}$ and never get out of it again! The same would happen if two nodes link to each other exclusively.

In order to overcome this «juice leak» we add the so-called «damping-factor» to the equation of one single iteration:

$w_{i} = \frac{1-d}{n} + d\cdot\sum_{j=1}^{n} \frac{M_{ji}}{n_{j}} w_{j}$

The damping-factor (usually 0.85) will decrease the weight of incoming links a little, but add a constant value of $1-d$ divided by the number of pages $n$ with every iteration. This will guarantee that there is always some source of «base value» streaming into the system so that it doesn’t dry out because of leaky pages.

This will lead to our final iteration formula^³:

$\vec{w}(k) = (1 - d) \cdot \sum_{j=0}^{k-1}d^{j}M^{j}\begin{bmatrix}1\\1\\1\\1\\1\end{bmatrix} + d^{k}M^{k}\vec{w}(0)$

With increasing $k$ the equilibrium i.e. the Eigenvector will be found at:

$\begin{bmatrix}0.15 \\ 0.21375 \\ 0.522938 \\ 0.594497 \\ 0.15 \end{bmatrix}$

This shows that our web page $W_{4}$ will be ranked highest (where all the votes end up) while $W_{1}$ and $W_{5}$ will be ranked lowest (because they don’t even have inbound links).

Demonstrating the Page Rank Algorithm

Let’s demonstrate the algorithm with a little Python program:

First, let’s define a dictionary that holds the descriptions of our web pages:

PAGES = {
    'grumpy-cats': {
        'title': 'Grumpy Cats',
        'links-to': (
            'best-three-cat-sites',
        )
    },
    'fluffy-cats': {
        'title': 'Fluffy Cats',
        'links-to': (
            'best-three-cat-sites',
        )
    },
    'just-lol-cats': {
        'title': 'Just Lol-Cats',
        'links-to': (
            'cat-videos',
            'best-three-cat-sites',
        )
    },
    'cat-videos': {
        'title': 'Best cat videos on the planet',
        'links-to': (
            'grumpy-cats',
            'best-three-cat-sites'
        )
    },
    'best-three-cat-sites': {
        'title': 'The three best cat sites',
        'links-to': (
            'grumpy-cats',
            'fluffy-cats',
            'just-lol-cats'
        )
    }
}

Next, we define a PageRanker class to unify all functionality related to our calculations. In order to calculate the page rank of our page defined above, we simply call the class method execute_pageranking(). Let’s look at what this method does:

@classmethod
def execute_pageranking(cls, k=500, d=0.85):

    unit_vec = cls.__build_unit_vector(len(PAGES.keys()))
    w = cls.__build_unit_vector(len(PAGES.keys()))
    adj = cls.__build_adjacency_graph()

    result_vec = (1 - d) * sum([d ** j * adj ** j * unit_vec for j in range(0, k - 1)]) + d ** k * adj ** k * w

    cls.__print_results(result_vec)

Obviously, our formula is on the second last line of this code snippet. Before we run it, we create a unit vector unit_vec with the number of dimensions set to the number of pages. The w vector will be exactly the same, with the only difference that it changes over the course of the iterations whereas unit_vec is going to stay the same and provide a constant source of «link juice» to keep our graph alive. The adj field will hold our Markov-adjacency matrix. We will see how it’s built shortly. The last method call is self-explanatory.

After the iterations, the result_vec field will hold an approximation of the Eigenvector, or in other words, the «balanced» score of our graph.

The __build_adjacency_graph method looks like this:

@staticmethod
def __build_adjacency_graph():

    matrix_rows = []

    for tp, (tp_id, tp_info) in enumerate(PAGES.items()):

        row = [0] * len(PAGES.keys())

        for sp, (sp_id, sp_info) in enumerate(PAGES.items()):

            outbound_links = sp_info.get('links-to', ())
            if tp_id in outbound_links:
                row[sp] = 1.0 / len(outbound_links)

        matrix_rows.append(row)

    return np.matrix(matrix_rows)

The first loop iterates over our target pages, i.e. the matrix’ rows. In order to fill one row, a second loop iterates over the source pages from where the links emerge. If the links defined in the source page contain our current target page, the partial vote value is calculated by dividing 1 by the total number of links on the source page and storing the value in the corresponding column.

With the default settings of 50 iterations and a damping factor of 0.85, the algorithm will give us:

Page Rank Results:
==================

Rank  Page name                       Page rank value
-----------------------------------------------------
1     The three best cat sites        2.09990987303
2     Grumpy Cats                     0.943278777045
3     Just Lol-Cats                   0.744970935429
4     Fluffy Cats                     0.744970935429
5     Best cat videos on the planet   0.466608510247

As expected, the page «The three best cat sites» is top-rated because every other page links to it. «Grumpy cats» is second because it is referenced from the important top-rated page and also from another page. The two inbound links makes it superior to the two other pages that are linked from the top-rated page.

Let’s see what happens if we remove the link from the top-rated page pointing to the «Grumpy Cats» page:

    {...},
    'best-three-cat-sites': {
        'title': 'The three best cat sites',
        'links-to': (
            # 'grumpy-cats', <---- Removed 
            'fluffy-cats',
            'just-lol-cats'
        )
    }

Page Rank Results:
==================

Rank  Page name                       Page rank value
-----------------------------------------------------
1     The three best cat sites        2.01442192032
2     Just Lol-Cats                   1.00612146063
3     Fluffy Cats                     1.00612146063
4     Best cat videos on the planet   0.577597280469
5     Grumpy Cats                     0.395476909134

Again, as expected, our «Grumpy Cats» page takes a deep dive as soon as a top-rated page decides to no longer include it as a link. It’s even on the last position because «Best cat videos» at least gets referenced from a more important page «Just Lol-Cats» which iself is referenced by the top-rated page.

Let’s say the owners of «Grumpy Cat» get really sad about this and decide to remove their link to «The three best cat sites» in return:

    'grumpy-cats': {
        'title': 'Grumpy Cats',
        'links-to': (
            # 'best-three-cat-sites', <------- removed
        )
    },
    {...}

Page Rank Results:
==================

Rank  Page name                       Page rank value
-----------------------------------------------------
1     The three best cat sites        1.13303700395
2     Just Lol-Cats                   0.631540876989
3     Fluffy Cats                     0.631540876989
4     Best cat videos on the planet   0.418404952215
5     Grumpy Cats                     0.327822147305

Even though this somewhat seems to have an effect on the rating, the ranking is not affected because the pages are all connected and suffer the same – even «Grumpy Cats» itself.

Since «Grumpy Cats» is now a dead end, we are really happy about that damping factor. Watch what happens when we disable it (i.e. set $d=1$ ):

Page Rank Results:
==================

Rank  Page name                       Page rank value
-----------------------------------------------------
1     The three best cat sites        0.070738758418
2     Just Lol-Cats                   0.0376406375322
3     Fluffy Cats                     0.0376406375322
4     Best cat videos on the planet   0.0200272965764
5     Grumpy Cats                     0.0106568686888

The overall rank value decreases significantly. If we increase the iterations to $k=1000$ :

Page Rank Results:
==================

Rank  Page name                       Page rank value
-----------------------------------------------------
1     The three best cat sites        1.53528832502e-27
2     Just Lol-Cats                   8.16909854913e-28
3     Fluffy Cats                     8.16909854913e-28
4     Best cat videos on the planet   4.34668654858e-28
5     Grumpy Cats                     2.31282360446e-28

our «link juice» has practically vanished.

References

https://www.google.com/patents/US6285999 ↩
https://www.youtube.com/watch?v=4wTHFmZPhT0 ↩
Teschl, Gerald & Susanne (2013): «Mathematik für Informatiker», 4. Auflage, Springer Verlag ↩

Linear Algebra Exercises

This is the documentation for my solutions to the Exercises of the course "Linear Algebra" at the Fernfachhochschule Schweiz (FFHS).